Getallen die ontaarden
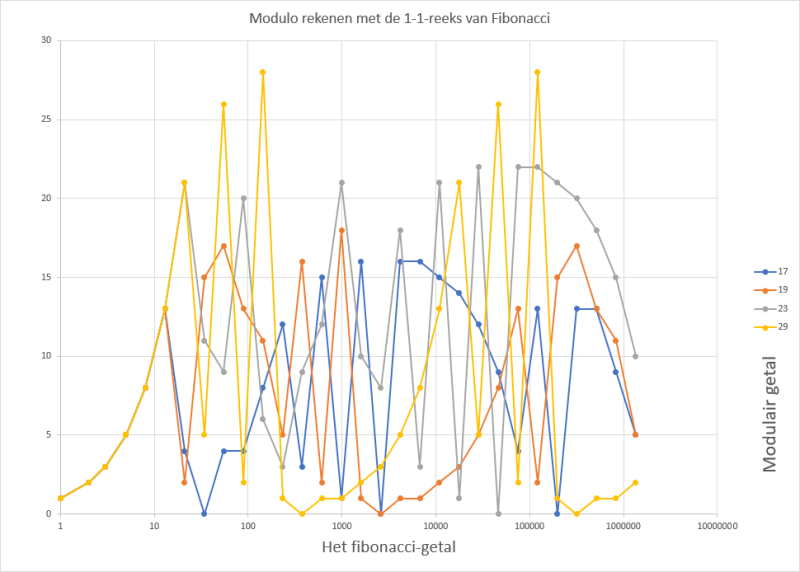
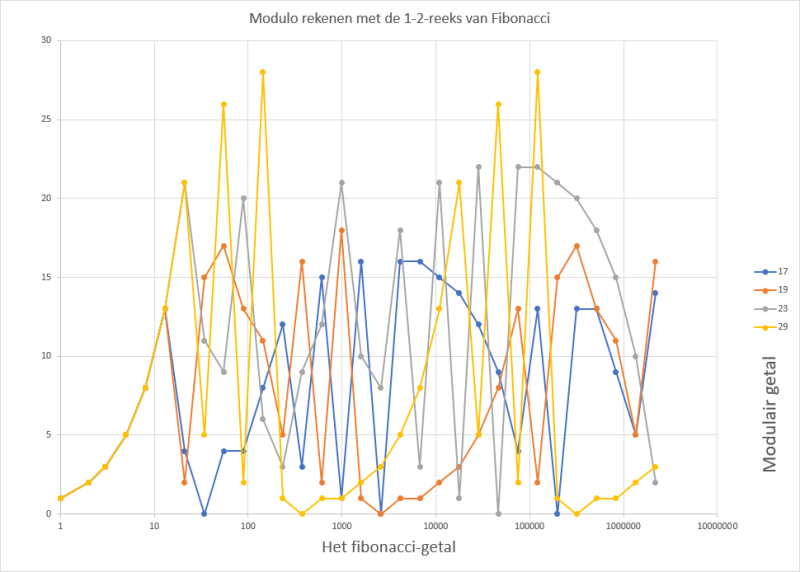
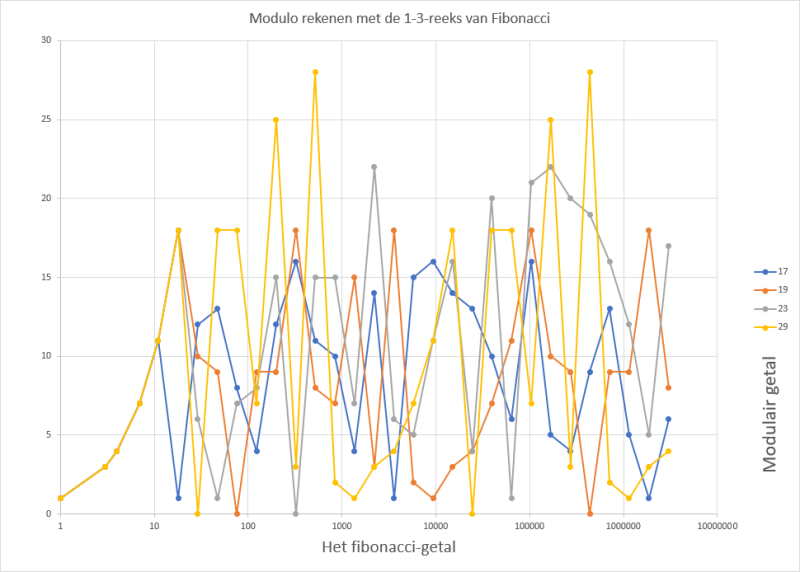
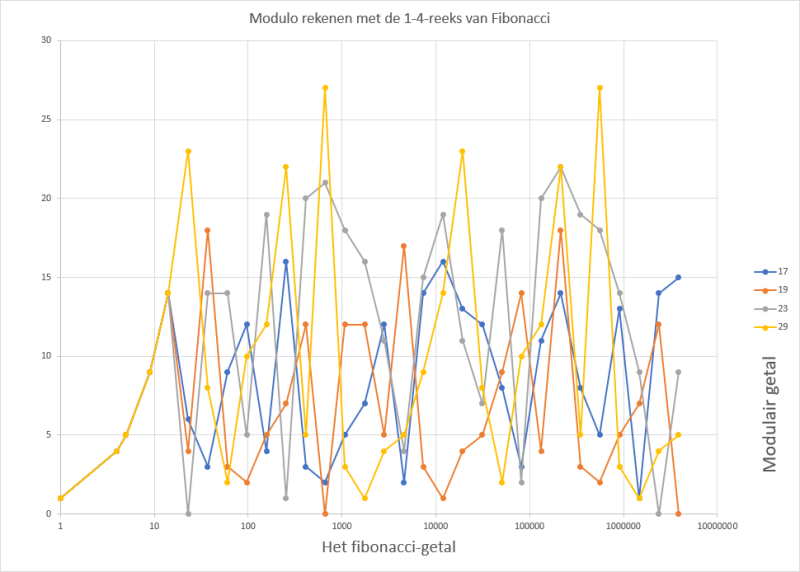
De reeks van Fibonacci kent iedereen wel (1,1,2,3,5,8,13,21,34,55,89,144,...). Elk getal is de som van de 2 vorige getallen. Wanneer we gewone muzieknoten willen gebruiken om deze te verklanken zitten we met het probleem dat de grootte van de getallen vrijwel meteen ontaardt. In de elektronische instrumenten worden noten met een nummer van 0 tot 127 aangeduid, daar zitten we bij het 12de fibonaccigetal al boven.
Modulo
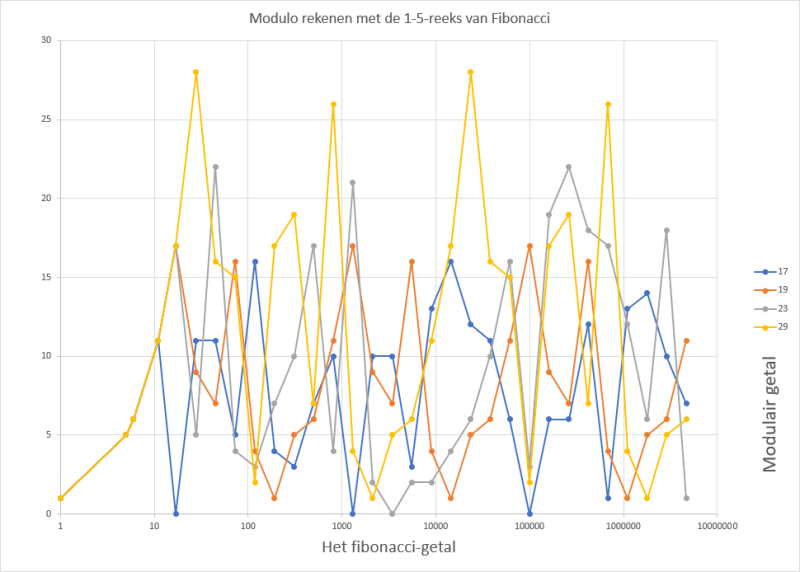
Deze getallenreeks wordt bruikbaarder als we ze via modulorekenen herleiden tot bruikbare toonhoogtes. Een modulo-interval kan bijvoorbeeld overeenkomen met beschikbare noten op een instrument of met geluidsfrequenties. Alle intervallen blijken repetitieve patronen voort te brengen. Kleinere intervallen hebben meestal kortere repetities en liggen (te?) gemakkelijk in het oor.
Voor wie niet vertrouwd is met modulorekenen: de klok is een mooi voorbeeld van een modulo-12 rekening. De uren blijven maar bijkomen, maar de klok herbegint met tellen vanaf 12)
Simulatie
Ik heb in Max/Msp een simulatie geprogrammeerd waarbij de getallen uit de fibonaccireeks als (midi)noten kunnen beluisterd worden dankzij een wijzigbaar modulo-interval M. Het programma werkt met startnoten A en B.
Video
Bekijk en beluister hierbij de video. Ik maak daarin ook gebruik van presets (rechthoek met blauwe bolletjes) die ik tijdens mijn verkenning vooraf heb opgeslagen
laatste update: 2021.05.19